Get rid of "L" shape when creating walls now!

[SalamanderRobot]

@Darkness01101

I’d just want the game to snap to the possible angles it can make the wall at.

For example, if we go with (a) where straight line is the default, then wherever you drag your mouse, the game will snap the straight wall to its eligible angles to show you where it can be constructed. This is how the game currently operates. The only difference I propose from current game in (a) is that you will never see it go to the L-shape while dragging your mouse around.

Sorry, but I still do not totally understand it. The only angles the game can make are multiple of 45° (horizontal, vertical, diagonal). It means that for most end points combinations, the wall will not be finished.

Are you talking about something similar to the following gif (made with the CodePen tool, grey is the suggested wall position while maintaining the mouse left button) ?

In comparison, the first solution of the ‘Salamander algorithm’ (1. diagonal attached to the first point (then horizontal or vertical)) would give this:

This is the same scenario, but with the comparison to the game current implementation (yellow is the game current implementation, grey is the ‘Salamander algorithm’):

As can be seen, there is a huge flip of the L-shape direction when close to the diagonal, which is not the case with the ‘Salamander algorithm’.

A last point to consider is that there are two solutions for the diagonal solutions and also two solutions for the L-shape solutions, because there is a central symmetry.

An option to switch between these two symmetrical solutions can also be useful (and is currently missing, even for the L-shape solutions).
Here is an example where I try to finish the wall (grey squares) to surround the buildings (brown squares) with a minimal number of additional tiles (so only the diagonal solutions) but still while maximizing the area being surrounded. Depending on the terrain configuration, I choose one or the other symmetrical solution.

@Darkness01101

The fact that I’m able to do this in one L-shaped action makes me a very happy AoE2 player…

I agree that there are some rare situations where a L-shape wall would be the best solution (but for me it is way less than 30% ). This is why the two symmetrical L-shapes solutions are also integrated in the ‘Salamander algorithm’, but they are the last (i.e. third and fourth) solutions when switching between the solutions.

At the same time, I also agree with @blastonguart that it can still easily be achieved with the diagonals solutions:

@blastonguart

Contrariwise, if the game forced optimal diagonals and you wanted to build an L, all you’d have to do is shift + click two more points — a massively easier operation.

[BubblyMango3400]

exactly!
even if you need an L shaped wall, the automatic L shape creates 1 extra wall unnecessarily at the corners. It takes both vil construction time and resources.

[SvenSvensonn]

@SalamanderRobot

I did not exactly understand your example. Could you maybe post a screenshot of this? You can for instance use the ‘Salamander thing’ tool with the Clear Map and draw options to draw something describing it.

Most of the times this is what happens; if you drag towards a solid the algorithm will add 1 unintended tile if you’re slightly off.

I should have tried your tool to be more exact in the wording of my issue, it seems that your tool does not create this excess tile. However still it creates 1 shifted tile which is not intended and creates a weakspot in the wall (more surface area to attack).

For this reason I think the default dragging of walls should always be in a straight line. I would suggest your feature to be optional behind a toggle setting or a modifier such as shift.

Also I would like to stress that if your salamander algorithm gets implemented, the L suggestions should NOT be part of the scrolling options. That’s exactly what we want to avoid and they would heavily mess with the efficiency of this feature.

Imagine if you want to create a big L (which is hardly ever the best solution), why would you do this by dragging a diagonal instead of 2 lines? The whole idea doesn’t make any sense.

@Darkness01101 You must have thought very long to come up with that extremely ridiculous and niche example. It’s not even done efficiently, look how much stone you wasted on that top wall. Everyone else would do that in 2 seperate lines to guarantee full controll, save time, resources and avoid likely errors caused by the L algorithm.

[Darkness01101]

@SvenSvensonn

@Darkness01101 You must have thought very long to come up with that extremely ridiculous and niche example. It’s not even done efficiently, look how much stone you wasted on that top wall. Everyone else would do that in 2 seperate lines to guarantee full controll, save time, resources and avoid likely errors caused by the L algorithm.

Yeah, took a whole 0.25 seconds. Was really challenging. No, it was easy because I play different maps than you and make different gameplay decisons than you. Ahh, the beauty of an RTS gane with so many options. Variety is the spice of life, Sven

[SvenSvensonn]

Then you realise you are in the vast minority, which makes your plea for keeping the status quo even more bizarre. Instead of listening to what everyone else seems to agree on, that there are better alternatives for the default behavior.

This has nothing to do with variety, rather with priority and optimising features according to how most play the game.

I play different maps than you

I don’t see how this is relevant.

I make different gameplay decisons than you.

I noticed!

[SalamanderRobot]

@SvenSvensonn

I should have tried your tool to be more exact in the wording of my issue, it seems that your tool does not create this excess tile. However still it creates 1 shifted tile which is not intended and creates a weakspot in the wall (more surface area to attack).

I understand that it is often not the desired output, but it is sometimes still what is expected.
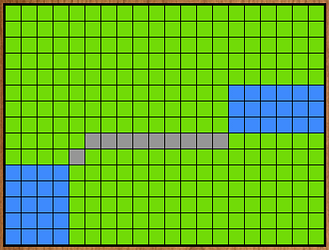
For instance, in this example, I want to add a minimal wall (grey) between the two water spots (blue).

Keeping the straight line would leave a hole in the wall.

Therefore, it is important to always join the two end points after dragging the mouse (even if sometimes we are slightly off).

@SvenSvensonn

I would suggest your feature to be optional behind a toggle setting or a modifier such as shift.

They implemented the toggle setting for the new way point system, so I assume it would be the same here.

@SvenSvensonn

Also I would like to stress that if your salamander algorithm gets implemented, the L suggestions should NOT be part of the scrolling options. That’s exactly what we want to avoid and they would heavily mess with the efficiency of this feature.

Imagine if you want to create a big L (which is hardly ever the best solution), why would you do this by dragging a diagonal instead of 2 lines? The whole idea doesn’t make any sense.

I agree that it is not needed (it was not even there in the initial post). Both options (including the L-shapes or not) are fine for me.

[Darkness01101]

@SvenSvensonn

Then you realise you are in the vast minority, which makes your plea for keeping the status quo even more bizarre. Instead of listening to what everyone else seems to agree on, that there are better alternatives for the default behavior.

Not sure what you mean. My latest posts say I want my idea of: “(a) ‘straight line only’ as the default with a modifier key to make the L-shape”"… which is definitely not status quo. And which would be optimizing it for the players you refer to.

[SvenSvensonn]

Yes sometimes we want to connect 2 points, sometimes we want a straight line. What matters is that our expectation matches the end result. For this reason a toggle in settings and/or modifier would be great.

My presented issue could be minimized if the algorithm wouldy stop altering the shape when you hover outside of the wallable area. So when dragging perfectly straight towards the edge of the map (or any solid), going off that straight line when outside of the map does not effect the shape off the wall. Perhaps this layer of complexity is not possible, but it came to mind.

@Darkness01101

You have no clue what I mean because apparently you made a 180 in your last post? I’m not gonna pretend like I read your posts past the first one or two. You’re really something else.

[Darkness01101]

@SvenSvensonn

You have no clue what I mean because apparently you made a 180 in your last post? I’m not gonna pretend like I read your posts past the first one or two. You’re really something else.

Sven, catch up. If you can’t bother to read posts or work positively with someone to understand their meaning before condescendingly lashing out at them (as you’ve done multiple times), then don’t post. Your negativity and bullying ways aren’t welcome here. I have no clue why you keep verbally jabbing. Please stop

[BoughtRelic9282]

@SalamanderRobot the more I read your posts here the better I like your idea, very creative! At first I didn’t quite grasp it but now I’m seeing how it would pretty much be better in every way haha.

Also i appreciate your constructive input into the conversation, and your thoughtful poise in response to ney-sayers. Keep up the great work of improving the community!

[SalamanderRobot]

@SvenSvensonn

So when dragging perfectly straight towards the edge of the map (or any solid), going off that straight line when outside of the map does not effect the shape off the wall. Perhaps this layer of complexity is not possible, but it came to mind.

Maybe something could be done as a special case for the edge of the map (to see what excatly).
This would be fine for me, but it might add an extra layer of complexity for players not following this thread (why does my wall sometimes connect two points, sometimes not ?).

The suggestion of the ‘Salamander algorithm’ is to always connect the two end points (i.e. similarly to the current algorithm), but doing it using the optimal (in terms of wall tiles count and fidelity to the straight line) configuration.
Adding extra rules might make it more difficult to grasp for many players.

@BoughtRelic9282

@SalamanderRobot the more I read your posts here the better I like your idea, very creative! At first I didn’t quite grasp it but now I’m seeing how it would pretty much be better in every way haha.

Great!

[Guanfranco]

Agreed please do this DE

[PalmSolo4448]

Disagree. Diagonal walls “leak”, I hate them…

[SalamanderRobot]

What do you mean? How do they leak more than horizontal or vertical walls?

[PalmSolo4448]

The flat edges, connected edge to edge, especially on even terrain, create a stronger less penetrable wall. I’ve used the point to point edges in diagonal walls, heard the warning horn and seen a cluster of AI units pushing through, not chopping down these tip to tip walls. And before you say the code is as impenetrable on a diagonal wall as a horizontal wall, my friends and I have all seen it happen, especially on uneven terrain. Each wall segment still requires the same amount of beatings to break but the leaking or squirting of a few troops prevents us from using diagonal walls unless going 2-4 rows deep.

[SalamanderRobot]

Are you sure this is not something related to a hole in the wall?

If not, it would seem more like a bug (if I remember properly a previous update indeed generated similar issues, but was solved).
Could you try to reproduce it? If you see it again, you can open a bug topic describing it (use images-videos from a replay where this happens).

[PalmSolo4448]

I’ll try but I heard that it’s darned impossible to get a good long diagonal wall without it going in to an “L”… lol

[Darkness01101]

@PalmSolo4448

I’ll try but I heard that it’s darned impossible to get a good long diagonal wall without it going in to an “L”… lol

Does that happen to you in single-player games vs. AI while not on a server, too? Would be interested to know if it is experienced or is as bad in single-player games, too

[Jarazz3343]

Last update introduced exactly those walls!

[PacificWheel208]

Probably most excited about this change, big improvement in the diagonal direction. However kind of underwhelming without the abillity to change wall direction on scroll.