Here is the initial message of my post QoL for walls optimal building (with algorithm):
When placing a wall connecting two points, the game will only use a diagonal configuration when the two end points are located on the same diagonal.
For example, in the following image, I would like to have a wall connecting the positions of the two monks. This is the automatic wall placement computed by the game:
This is not optimal for two reasons:
- It requires 13 tiles, for a total cost of 13 * 5 = 65 stones.
- It is far from the ideal straight line between the two points. Therefore, the deviation from this straight line often results in tiles of the wall placed in locations already occupied (by buildings, natural elements…).
A better solution (Solution 1) is the following:
Here, we have a 8 tiles wall (40 stones), with a smaller deviation from the ideal straight line (and thus, less likely to be located on occupied tiles).
An equivalent solution (also 8 tiles for 40 stones) can be achieved with the following solution (Solution 2):
The current behavior is usually not the best one and requires most of the time to spend time in order to properly place each diagonal wall separately (by finding the perfect tile).
Moreover, when we fail to correctly place the wall, we have to manually delete each construction tile, which requires even more time.
The implementation of the aforementioned optimal wall placement can be achieved as follows:
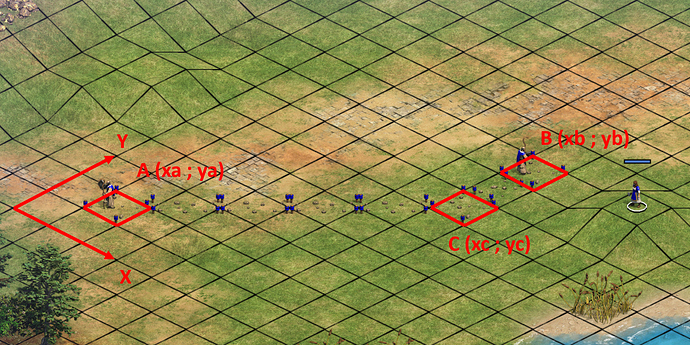
In the next image, we want to join point A (with coordinates (xa ; ya)) to point B (xb ; yb), possibly by computing an intermediate point C (xc ; yc).
We start by computing dx = xb - xa and dy = yb - ya.
- dx = dy = 0 -> 1x1 tile
- dx = 0 -> vertical wall
- dy = 0 -> horizontal wall
- dx = dy or dx = -dy -> diagonal wall
All the aforementioned cases correspond to the current behavior (and require no adaptation).
In the other cases, we need to compute the point C (xc ; yc). Then, the two junctions A-C and C-B can be computed as described above, using straight lines.
Currently, the game computes it as C = (xa ; yb) if abs(dy) > abs(dx) (see first image), or (xb ; ya) otherwise.
To achieve the Solution 1 (i.e. diagonal section attached to point A), we compute it as:
- d = min(abs(dx), abs(dy))
- xc = xa + sgn(dx) * d
- yc = ya + sgn(dy) * d
where:
- sgn(x) is -1 for x < 0, +1 otherwise
- abs(x) is the absolute value of x
- min(x, y) returns the minimal value between x and y
To achieve the Solution 2 instead (i.e. diagonal section attached to point B), we compute it as follows:
- if abs(dx) > abs(dy)
- xc = xa + sgn(dx) * (abs(dx) - abs(dy))
- yc = ya
- otherwise
- xc = xa
- yc = ya + sgn(dy) * (abs(dy) - abs(dx))
So, adaptations could be quite straightforward as only the computation of point C (xc ; yc) must be adapted.
It could make the placement of walls faster, more intuitive (thinking about straight lines between points) and more efficient in term of stone cost (or wood cost for palisade).
In case the current behavior is the one requested, it is still possible to queue wall parts with shift.!